Linear Trend

Linear trend is a simple function described as a straight line along several points of time series value in time series graph. Linear trend has a common pattern:

T_t = a + b.Y_t

Where
T_t = Trend value of period t
a  = Constant of trend value at base period
b  = Coefficient of trend line direction
Yt = an independent variable, represents time variable, usually assumed to have integer value
       1,2,3,... as in the sequence of time series data.

There are several methods that can be used to find the linear trend equation of a time series. Most commonly used is least squares method. This method finds the coefficient values of the trend equation (a and b) by minimizing mean of squared error (MSE). The formula is:

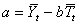
Nonlinear Trend

In several cases, linear trend is not suitable for time series data. These cases occur when a time series has a different gradient between the beginning phase of the data and the next phase. For these cases, it is better to use nonlinear trend than linear trend.

There are several nonlinear trends, they are:

• Exponential

       T_t = ab^y

• Quadratic

       T_t = a + bY_t + cY_t²

• Cubic

       T_t = a + bY_t + cYt_t² + dY_t³

The most suitable trend is a one with the smallest error, that is the smallest difference between actual data and estimated data from trend value. The common rule used to find the best trend is by choosing a trend with the smallest standard error value and having the biggest R-square value.